Divorce Analysis: Key Factors & Insights
Home // AI-Powered Data Analysis
🔎 Introduction
This project provides a data-driven analysis of divorce trends, identifying key risk factors and extracting actionable insights. Using statistical analysis, machine learning models, SQL queries, and Power BI visualizations, we explored financial, educational, demographic, and behavioral patterns that influence marriage stability.
📋 Project Overview
📌Project Objectives
- Identify key risk factors for divorce
- Analyze financial, educational, and demographic influences
- Develop predictive models for estimating marriage duration
- Create SQL databases and Power BI dashboards for business insights
📌 Dataset Description
This analysis is based on real-world divorce data, containing:
- 2,209 divorce records
- 10 key attributes covering:
- Demographics: Spouse age, number of kids
- Financial Data: Income levels
- Marriage & Divorce Dates: To calculate marriage duration
📌Methodology & Data Processing
- Data Cleaning: Handle missing values, drop duplicated rows and detect outliers.
- Feature Engineering : Add new columns and data transformation
- Exploratory Data Analysis (EDA): Statistical insights & visual trends.
- Machine Learning: Predictive modeling for marriage duration.
- SQL Insights: Query-based analysis on key divorce patterns.
- Power BI Dashboard: Interactive visualization for decision-making.
📌 Expected Outcomes
- A structured understanding of divorce trends based on data.
- Insights into financial & educational impacts on marriage stability.
- Predictive analytics for estimating marriage duration.
- Data-driven recommendations for relationship stability & policy insights.
❓ Key Business Questions
❓ Which income levels and education backgrounds are most associated with higher divorce rates?
❓ Are there common patterns in marriage duration before divorce?
❓ Does household income affect marriage stability?
❓ Do income differences between partners correlate with divorce?
❓ Are younger or older couples more likely to divorce?
❓ Can we build a predictive model for marriage duration before divorce?
These questions guide my data analysis, uncovering key insights into marriage stability and divorce patterns.
📊 Summary of the Dataset
🗂️ Key Dataset Attributes
- Total Records: 2,209 divorces
- Total Columns: 10 features
- Time Period Covered: Includes marriage and divorce records over multiple years
👨👩👦👦 Demographic Information
- dob_man & dob_woman: Birthdates of husband and wife, used to calculate age at marriage and divorce.
- num_kids: Number of children in the marriage, which may influence marriage stability.
💸 Financial Data
- income_man & income_woman: Annual income for both partners, impacting financial stability in marriage.
🎓 Educational Background
- education_man & education_woman: Education levels attained, influencing career opportunities and financial stability.
💔 Marriage & Divorce Data
- marriage_date: The date the couple got married.
- divorce_date: The date the couple got divorced.
- marriage_duration: Number of years before divorce, critical for analyzing stability patterns.
🧹Data Cleaning & Preparation
Load the dataset & check for missing values
# Load the dataset and check its structure
import pandas as pd
# Load the dataset
divorce = pd.read_csv(r'D:\roy\roy files\Data\data project\divorce.csv')
# Display general info and missing values
dataset_info = {
"Total Rows": df.shape[0],
"Total Columns": df.shape[1],
"Missing Values per Column": df.isnull().sum().to_dict(),
"Duplicate Rows": df.duplicated().sum(),
"Data Types": df.dtypes.to_dict()
}
# Display dataset summary
pd.DataFrame(dataset_info)
| Total Rows | Total Columns | Missing Values per Column | Duplicate Rows | Data Types | |
|---|---|---|---|---|---|
| divorce_date | 2209 | 10 | 0 | 0 | object |
| dob_man | 2209 | 10 | 0 | 0 | object |
| education_man | 2209 | 10 | 4 | 0 | object |
| income_man | 2209 | 10 | 0 | 0 | float64 |
| dob_woman | 2209 | 10 | 0 | 0 | object |
| education_woman | 2209 | 10 | 0 | 0 | object |
| income_woman | 2209 | 10 | 0 | 0 | float64 |
| marriage_date | 2209 | 10 | 0 | 0 | object |
| marriage_duration | 2209 | 10 | 0 | 0 | float64 |
| num_kids | 2209 | 10 | 876 | 0 | float64 |
Handling Missing Values
# Fill missing values in num_kids with 0 (assuming missing means no children)
df.isna().sum()
df['num_kids'] = df['num_kids'].fillna(0).astype(int)
divorce_date 0
dob_man 0
education_man 4
income_man 0
dob_woman 0
education_woman 0
income_woman 0
marriage_date 0
marriage_duration 0
num_kids 0
dtype: int64
# Fill missing education levels for men based on the closest matching average income:
def fill_missing_education_man(df):
avg_income_man = df.groupby('education_man')['income_man'].mean()
def assign_education(income):
return avg_income_man.sub(income).abs().idxmin()
df.loc[df['education_man'].isna(),'education_man'] = \
df.loc[df['education_man'].isna(),'income_man'].apply(assign_education)
return df
df = fill_missing_education_man(df)
divorce_date 0
dob_man 0
education_man 0
income_man 0
dob_woman 0
education_woman 0
income_woman 0
marriage_date 0
marriage_duration 0
num_kids 0
dtype: int64
Converting Data Types
# Convert date columns to datetime format
date_columns = ['divorce_date', 'dob_man', 'dob_woman', 'marriage_date']
for col in date_columns:
df[col] = pd.to_datetime(df[col], errors='coerce')
divorce_date datetime64[ns]
dob_man datetime64[ns]
education_man object
income_man float64
dob_woman datetime64[ns]
education_woman object
income_woman float64
marriage_date datetime64[ns]
marriage_duration float64
num_kids int64
dtype: object
# Convert Education Columns to Categorical Format
df['education_man'] = df['education_man'].astype('category')
df['education_woman'] = df['education_woman'].astype('category')
divorce_date datetime64[ns]
dob_man datetime64[ns]
education_man category
income_man float64
dob_woman datetime64[ns]
education_woman category
income_woman float64
marriage_date datetime64[ns]
marriage_duration float64
num_kids int64
dtype: object
Detect Outliers using the IQR Method
# Define columns to check for outliers
outlier_columns = ['income_man', 'income_woman', 'marriage_duration']
# Compute IQR for each column
for col in outlier_columns:
Q1 = df[col].quantile(0.25)
Q3 = df[col].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
print(f"{col} - Lower Bound: {lower_bound}, Upper Bound: {upper_bound}")
print(f"Outliers: {df[(df[col] < lower_bound) | (df[col] > upper_bound)][col].count()}\n")
income_man - Lower Bound: -6000.0, Upper Bound: 19600.0
Outliers: 154
income_woman - Lower Bound: -4500.0, Upper Bound: 15500.0
Outliers: 120
marriage_duration - Lower Bound: -11.0, Upper Bound: 29.0
Outliers: 27
Creating an Outlier Flag Column
# Define columns and their outlier thresholds
outlier_columns = {
'income_man': (-6000, 19600),
'income_woman': (-4500, 15500),
'marriage_duration': (-11, 29)
}
# Create an 'is_outlier' column
df['is_outlier'] = 0 # Default to 0 (Not an Outlier)
# Flag records exceeding the threshold
for col, (low, high) in outlier_columns.items():
df.loc[(df[col] < low) | (df[col] > high), 'is_outlier'] = 1
Data Validation
print(df.info()) # Check final structure
print(df.isnull().sum()) # Ensure no missing values
print(df['is_outlier'].value_counts()) # Count flagged outliers
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2209 entries, 0 to 2208
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 divorce_date 2209 non-null datetime64[ns]
1 dob_man 2209 non-null datetime64[ns]
2 education_man 2209 non-null category
3 income_man 2209 non-null float64
4 dob_woman 2209 non-null datetime64[ns]
5 education_woman 2209 non-null category
6 income_woman 2209 non-null float64
7 marriage_date 2209 non-null datetime64[ns]
8 marriage_duration 2209 non-null float64
9 num_kids 2209 non-null int64
10 is_outlier 2209 non-null int64
dtypes: category(2), datetime64[ns](4), float64(3), int64(2)
memory usage: 160.2 KB
None
divorce_date 0
dob_man 0
education_man 0
income_man 0
dob_woman 0
education_woman 0
income_woman 0
marriage_date 0
marriage_duration 0
num_kids 0
is_outlier 0
dtype: int64
is_outlier
0 1951
1 258
Name: count, dtype: int64
⚙Feature Engineering
Creating New Columns
# 1️⃣ Age at Marriage for Man & Woman
df['age_at_marriage_man'] = df['marriage_date'].dt.year - df['dob_man'].dt.year
df['age_at_marriage_woman'] = df['marriage_date'].dt.year - df['dob_woman'].dt.year
# 2️⃣ Age at Divorce for Man & Woman
df['age_at_divorce_man'] = df['divorce_date'].dt.year - df['dob_man'].dt.year
df['age_at_divorce_woman'] = df['divorce_date'].dt.year - df['dob_woman'].dt.year
# 3️⃣ Income Difference (Man - Woman)
df['income_difference'] = df['income_man'] - df['income_woman']
# 4️⃣ Household Income (Sum of Both Spouses' Income)
df['household_income'] = df['income_man'] + df['income_woman']
# 5️⃣ Income Ratio (Man's Income Compared to Woman's)
df['income_ratio'] = df['income_man'] / df['income_woman']
df['income_ratio'].replace([float('inf'), -float('inf')], None, inplace=True) # Handle division by zero
# 6️⃣ Age Gap Between Spouses
df['age_gap'] = df['age_at_marriage_man'] - df['age_at_marriage_woman']
# 7️⃣ Marriage Stability Category (Short <5 years, Middle <=10 years, Long 10+ years)
df['marriage_stability'] = df['marriage_duration'].apply(
lambda x: 'Short' if x < 5 else ('Middle' if x <= 10 else 'Long')
)
df.head()
| divorce_date | dob_man | education_man | income_man | dob_woman | education_woman | income_woman | marriage_date | marriage_duration | num_kids | is_outlier | age_at_marriage_man | age_at_marriage_woman | age_at_divorce_man | age_at_divorce_woman | income_difference | household_income | income_ratio | age_gap | marriage_stability |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2006-09-06 | 1975-12-18 | Secondary | 2000.0 | 1983-08-01 | Secondary | 1800.0 | 2000-06-26 | 5.0 | 1 | 0 | 25 | 17 | 31 | 23 | 200.0 | 3800.0 | 1.1111111111111112 | 8 | Middle |
| 2008-01-02 | 1976-11-17 | Professional | 6000.0 | 1977-03-13 | Professional | 6000.0 | 2001-09-02 | 7.0 | 0 | 0 | 25 | 24 | 32 | 31 | 0.0 | 12000.0 | 1.0 | 1 | Middle |
| 2011-01-02 | 1969-04-06 | Preparatory | 5000.0 | 1970-02-16 | Professional | 5000.0 | 2000-02-02 | 2.0 | 2 | 0 | 31 | 30 | 42 | 41 | 0.0 | 10000.0 | 1.0 | 1 | Short |
| 2011-01-02 | 1979-11-13 | Secondary | 12000.0 | 1981-05-13 | Secondary | 12000.0 | 2006-05-13 | 2.0 | 0 | 0 | 27 | 25 | 32 | 30 | 0.0 | 24000.0 | 1.0 | 2 | Short |
| 2011-01-02 | 1982-09-20 | Professional | 6000.0 | 1988-01-30 | Professional | 10000.0 | 2007-08-06 | 3.0 | 0 | 0 | 25 | 19 | 29 | 23 | -4000.0 | 16000.0 | 0.6 | 6 | Short |
📈 Exploratory Data Analysis (EDA)
Exploratory Data Analysis (EDA)
Which income levels and education backgrounds are most associated with higher divorce rates?
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
# 1️⃣ Divorce Count by Education Level (Men vs. Women)
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Order of education categories for better readability
education_order = ['Primary', 'High School', 'Secondary', 'Professional', 'Other']
# Divorce count by men's education level
sns.countplot(data=df, x='education_man', order=education_order, ax=axes[0], palette="Blues")
axes[0].set_title("Divorce Count by Men's Education Level")
axes[0].set_xlabel("Education Level (Men)")
axes[0].set_ylabel("Divorce Count")
axes[0].set_xticklabels(axes[0].get_xticklabels(), rotation=30)
# Divorce count by women's education level
sns.countplot(data=df, x='education_woman', order=education_order, ax=axes[1], palette="Oranges")
axes[1].set_title("Divorce Count by Women's Education Level")
axes[1].set_xlabel("Education Level (Women)")
axes[1].set_ylabel("Divorce Count")
axes[1].set_xticklabels(axes[1].get_xticklabels(), rotation=30)
plt.tight_layout()
plt.show()
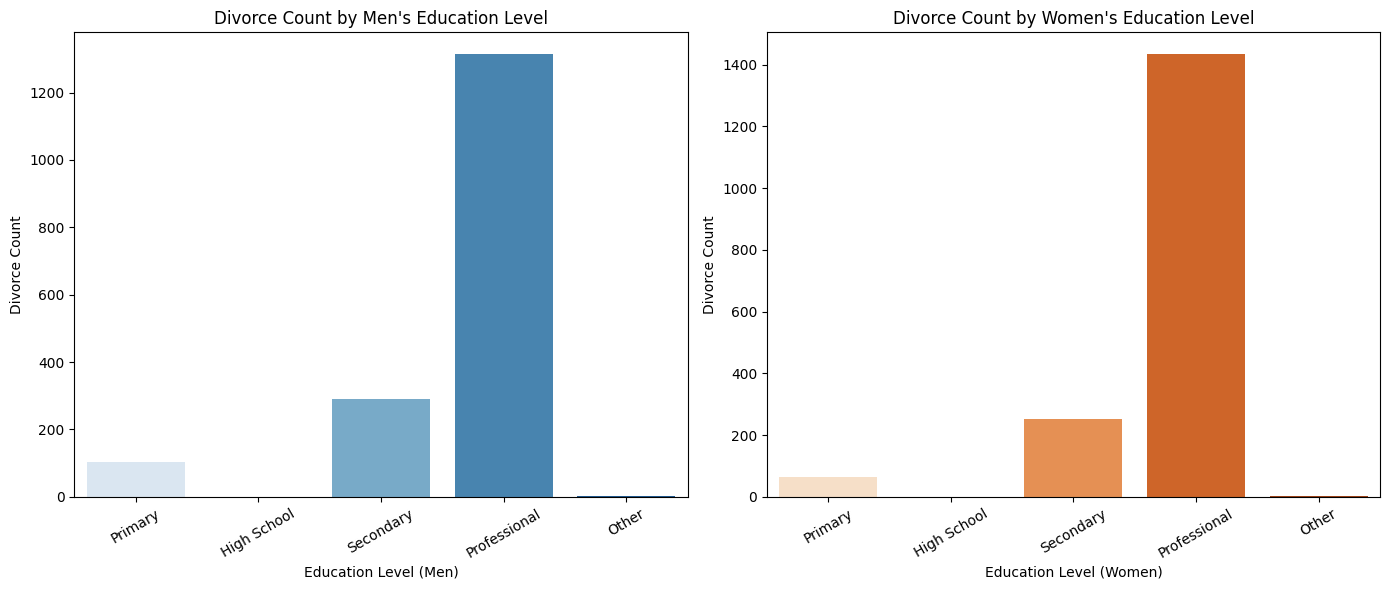
Higher divorce rates are observed among professionally educated individuals, especially women, possibly due to career demands and financial independence. In contrast, lower-educated individuals show fewer divorces, potentially influenced by traditional family values or economic dependence.
# 2️⃣ Divorce Count by Income Categories (Low < 20K, Middle 20K-30K, High > 30K)
df['income_category'] = df['household_income'].apply(lambda x: 'Low (<$20K)' if x < 20000 else ('Middle ($20K-$30K)' if x <= 30000 else 'High (>$30K)'))
plt.figure(figsize=(8, 6))
sns.countplot(data=df, x='income_category', palette="coolwarm", order=['Low (<$20K)', 'Middle ($20K-$30K)', 'High (>$30K)'])
plt.title("Divorce Count by Household Income Category")
plt.xlabel("Household Income Category")
plt.ylabel("Divorce Count")
plt.show()
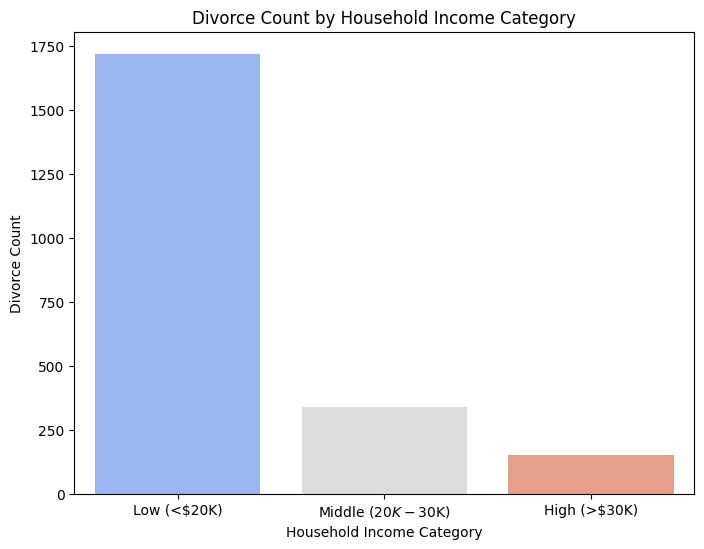
Divorce rates are significantly higher among low-income households, suggesting financial instability as a major factor in marital breakdowns. Higher-income groups experience fewer divorces, indicating better financial security may contribute to marriage stability.
# Encoding for Education Columns
education_mapping = {'Primary': 1, 'High School': 2, 'Secondary': 3, 'Professional': 4, 'Other': 5}
df['education_man_encoded'] = df['education_man'].map(education_mapping)
df['education_woman_encoded'] = df['education_woman'].map(education_mapping)
# Fill NaN values with the most frequent education level
most_common_edu_man = df['education_man_encoded'].mode()[0]
most_common_edu_woman = df['education_woman_encoded'].mode()[0]
df['education_man_encoded'].fillna(most_common_edu_man, inplace=True)
df['education_woman_encoded'].fillna(most_common_edu_woman, inplace=True)
# Convert back to integer
df['education_man_encoded'] = df['education_man_encoded'].astype(int)
df['education_woman_encoded'] = df['education_woman_encoded'].astype(int)
# 3️⃣ Correlation Analysis: Income & Marriage Duration
corr_income_duration, p_income_duration = stats.pearsonr(df['household_income'], df['marriage_duration'])
# 4️⃣ Correlation Analysis: Education & Marriage Duration (Using Encoded Education Levels)
corr_edu_man, p_edu_man = stats.pearsonr(df['education_man_encoded'], df['marriage_duration'])
corr_edu_woman, p_edu_woman = stats.pearsonr(df['education_woman_encoded'], df['marriage_duration'])
# Print correlation results
correlation_results = {
"Income vs Marriage Duration": {"Correlation": corr_income_duration, "P-Value": p_income_duration},
"Men's Education vs Marriage Duration": {"Correlation": corr_edu_man, "P-Value": p_edu_man},
"Women's Education vs Marriage Duration": {"Correlation": corr_edu_woman, "P-Value": p_edu_woman},
}
correlation_results
{'Income vs Marriage Duration': {'Correlation': np.float64(0.10116847509679286),
'P-Value': np.float64(1.8936462468448785e-06)},
"Men's Education vs Marriage Duration": {'Correlation': np.float64(-0.07246062770090014),
'P-Value': np.float64(0.0006539231763137255)},
"Women's Education vs Marriage Duration": {'Correlation': np.float64(-0.10966352322878775),
'P-Value': np.float64(2.380620476323242e-07)}}
The correlation results suggest that income has a weak positive correlation with marriage duration, indicating that higher household income slightly contributes to longer marriages. Men’s and women’s education levels both show weak negative correlations with marriage duration, implying that higher education, especially for women, is associated with slightly shorter marriages. However, the relationships are weak, and other factors may play a more significant role in determining marriage stability.
Are there common patterns in marriage duration before divorce?
import matplotlib.pyplot as plt
import seaborn as sns
# Set figure size
plt.figure(figsize=(10, 6))
# 1️⃣ Histogram of Marriage Duration
sns.histplot(df['marriage_duration'], bins=30, kde=True, color="blue")
plt.title("Distribution of Marriage Duration Before Divorce")
plt.xlabel("Marriage Duration (Years)")
plt.ylabel("Count")
plt.show()
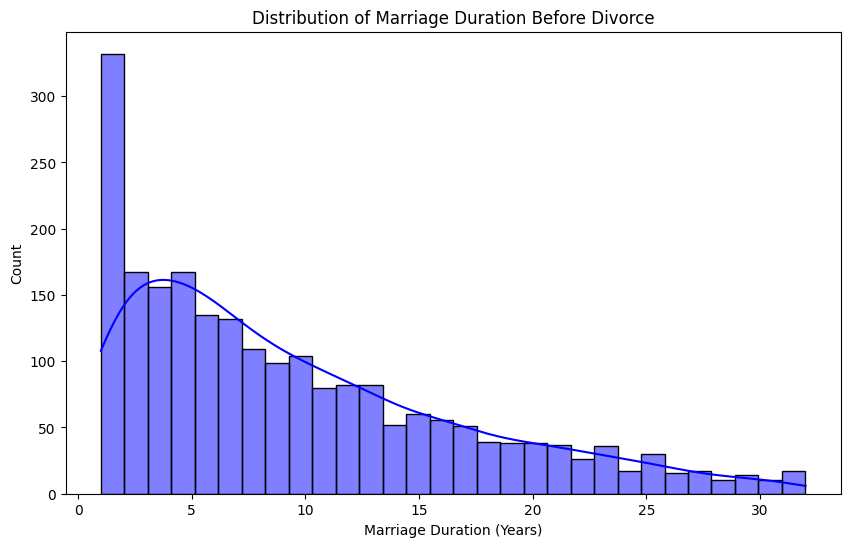
This histogram shows the distribution of marriage duration before divorce. The data is right-skewed, indicating that most divorces happen within the first few years of marriage, with a sharp decline as the duration increases. The highest frequency is observed at very short durations (0-5 years), reinforcing the trend that early divorces are more common. Longer marriages before divorce are much less frequent. This suggests that if a couple stays together beyond the early years, their chances of long-term stability increase.
# 2️⃣ Marriage Stability Distribution
plt.figure(figsize=(8, 5))
sns.countplot(data=df, x='marriage_stability', palette="coolwarm", order=["Short", "Middle", "Long"])
plt.title("Marriage Stability Distribution")
plt.xlabel("Marriage Stability Category")
plt.ylabel("Count")
plt.show()
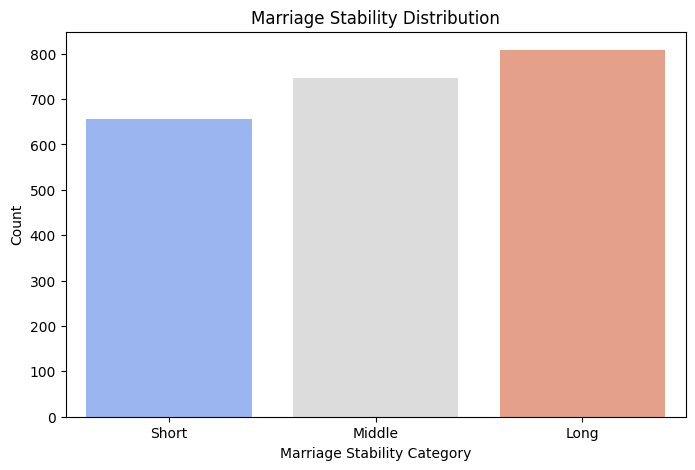
This bar chart illustrates the distribution of marriage stability categories. "Short" marriages (less than 5 years) account for a significant portion of divorces, but "Middle" (5-10 years) and "Long" (10+ years) durations also have substantial divorce counts. The trend suggests that while many divorces occur early, a considerable number also happen after a decade, indicating that long-term marital challenges still contribute to divorce.
# 3️⃣ Boxplot of Marriage Duration by Key Factors
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Marriage Duration by Number of Kids
sns.boxplot(data=df, x="num_kids", y="marriage_duration", ax=axes[0], palette="Blues")
axes[0].set_title("Marriage Duration by Number of Kids")
axes[0].set_xlabel("Number of Kids")
axes[0].set_ylabel("Marriage Duration")
# Marriage Duration by Income Category
sns.boxplot(data=df, x="income_category", y="marriage_duration", ax=axes[1], palette="Oranges")
axes[1].set_title("Marriage Duration by Income Category")
axes[1].set_xlabel("Income Category")
axes[1].set_ylabel("Marriage Duration")
plt.tight_layout()
plt.show()
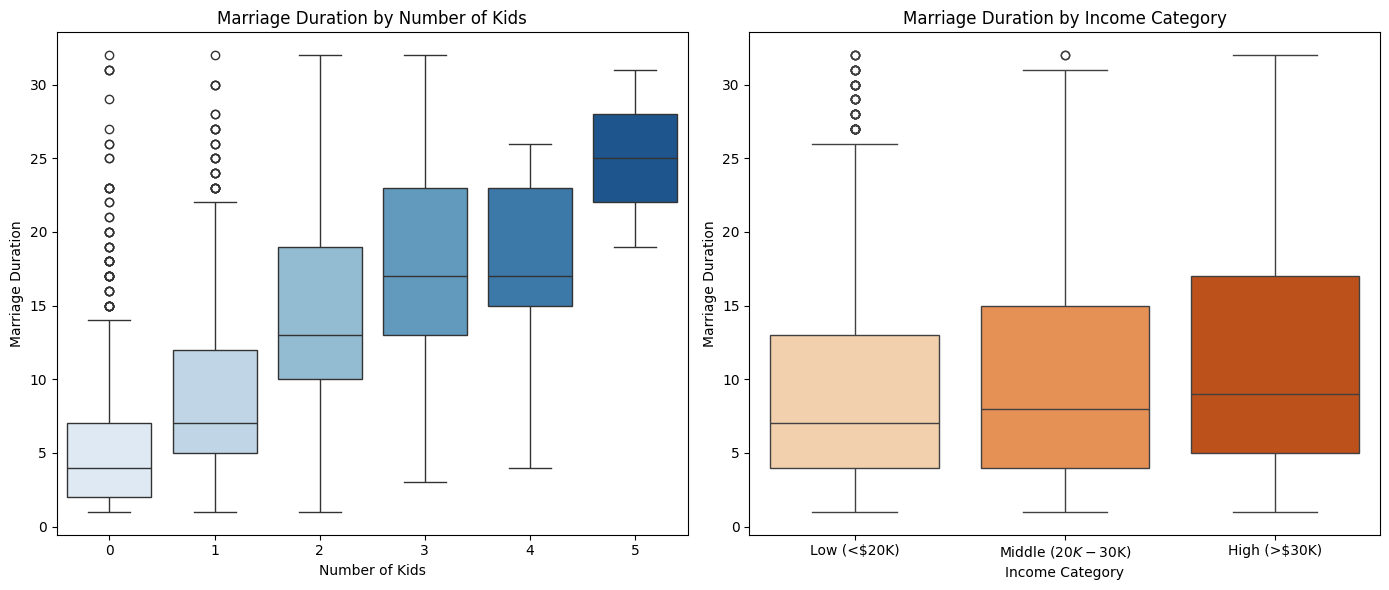
The left boxplot shows that marriage duration tends to increase with the number of children, indicating that couples with more kids are likely to stay married longer. The right boxplot reveals that income level has a weaker correlation with marriage duration, as all income groups show similar distributions, though higher-income couples exhibit slightly longer marriages on average.
Does household income affect marriage stability?
# Marriage stability distribution by income category.
# Set figure size
plt.figure(figsize=(8, 6))
# Create stacked bar chart for marriage stability by income category
income_stability_counts = df.groupby(['income_category', 'marriage_stability']).size().unstack()
# Plot
income_stability_counts.plot(kind='bar', stacked=True, colormap='coolwarm', figsize=(8, 6))
# Labels and title
plt.title("Marriage Stability Distribution by Income Category")
plt.xlabel("Household Income Category")
plt.ylabel("Count")
plt.xticks(rotation=0)
plt.legend(title="Marriage Stability")
# Show plot
plt.show()
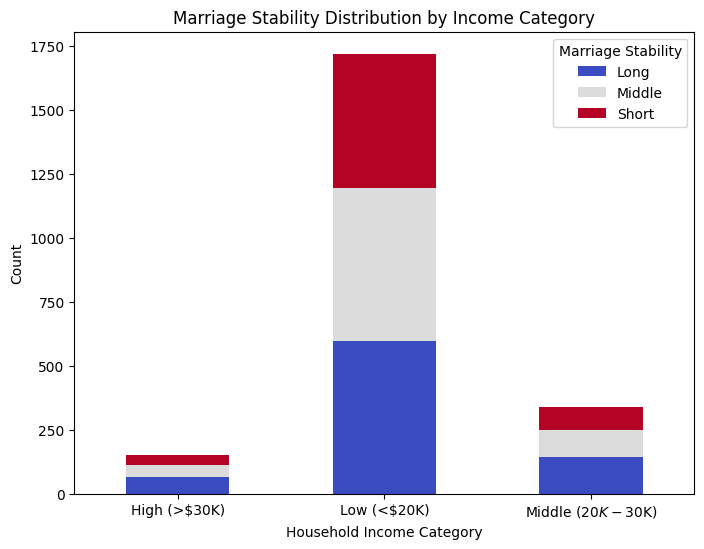
The majority of divorces occur in the low-income category (<$20K), with a significant portion having short or middle marriage durations. Higher-income couples (>$30K) tend to have longer marriages before divorce, suggesting financial stability may contribute to longer marriage durations.
# 2️⃣ Marriage Stability Distribution
plt.figure(figsize=(8, 5))
sns.countplot(data=df, x='marriage_stability', palette="coolwarm", order=["Short", "Middle", "Long"])
plt.title("Marriage Stability Distribution")
plt.xlabel("Marriage Stability Category")
plt.ylabel("Count")
plt.show()

This bar chart illustrates the distribution of marriage stability categories. "Short" marriages (less than 5 years) account for a significant portion of divorces, but "Middle" (5-10 years) and "Long" (10+ years) durations also have substantial divorce counts. The trend suggests that while many divorces occur early, a considerable number also happen after a decade, indicating that long-term marital challenges still contribute to divorce.
# 3️⃣ Boxplot of Marriage Duration by Key Factors
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Marriage Duration by Number of Kids
sns.boxplot(data=df, x="num_kids", y="marriage_duration", ax=axes[0], palette="Blues")
axes[0].set_title("Marriage Duration by Number of Kids")
axes[0].set_xlabel("Number of Kids")
axes[0].set_ylabel("Marriage Duration")
# Marriage Duration by Income Category
sns.boxplot(data=df, x="income_category", y="marriage_duration", ax=axes[1], palette="Oranges")
axes[1].set_title("Marriage Duration by Income Category")
axes[1].set_xlabel("Income Category")
axes[1].set_ylabel("Marriage Duration")
plt.tight_layout()
plt.show()

The left boxplot shows that marriage duration tends to increase with the number of children, indicating that couples with more kids are likely to stay married longer. The right boxplot reveals that income level has a weaker correlation with marriage duration, as all income groups show similar distributions, though higher-income couples exhibit slightly longer marriages on average.
Do income differences between partners correlate with divorce?
import matplotlib.pyplot as plt
import seaborn as sns
# Set figure size
plt.figure(figsize=(10, 6))
# Scatter plot with regression line
sns.regplot(
data=df,
x="income_difference",
y="marriage_duration",
scatter_kws={'alpha': 0.5},
line_kws={"color": "red"},
)
# Titles and labels
plt.title("Income Difference vs. Marriage Duration", fontsize=14)
plt.xlabel("Income Difference (Man - Woman)", fontsize=12)
plt.ylabel("Marriage Duration (Years)", fontsize=12)
# Show plot
plt.show()
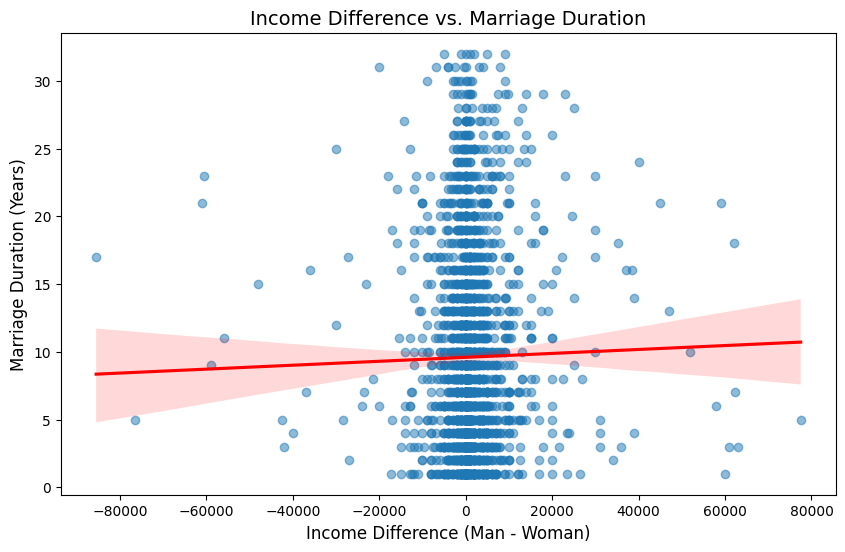
The scatter plot shows a weak positive correlation between income difference and marriage duration, suggesting that income disparity between spouses has minimal impact on how long a marriage lasts. Most divorces occur among couples with small income differences, while extreme income gaps (both high and low) do not significantly alter marriage duration trends.
# Define income ratio categories
df['income_ratio_category'] = df['income_ratio'].apply(lambda x:
'Equal (0.9 - 1.1)' if 0.9 <= x <= 1.1 else
'Man Earns More (>1.1)' if x > 1.1 else
'Woman Earns More (<0.9)')
# Group data for plotting
stability_income = df.groupby(['income_ratio_category', 'marriage_stability']).size().unstack()
# Plot stacked bar chart
stability_income.plot(kind='bar', stacked=True, colormap='coolwarm', figsize=(10, 6))
# Chart formatting
plt.title('Marriage Stability by Income Ratio')
plt.xlabel('Income Ratio Category')
plt.ylabel('Count')
plt.legend(title="Marriage Stability")
plt.xticks(rotation=20)
# Show plot
plt.show()
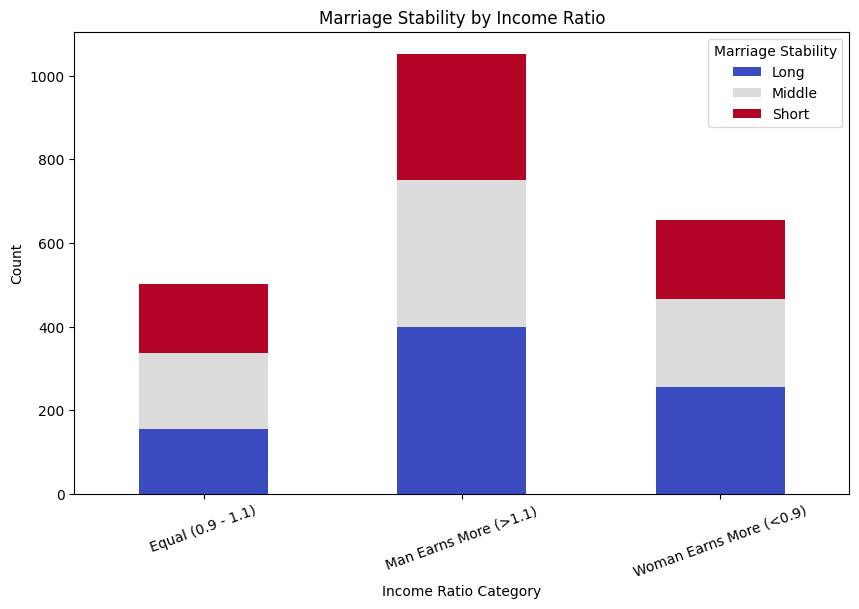
This chart illustrates the relationship between income ratio and marriage stability. Couples where the man earns significantly more (>1.1 ratio) have the highest divorce count, with a notable portion categorized as short marriages. In contrast, equal-income couples (0.9-1.1 ratio) and those where the woman earns more (<0.9 ratio) show relatively fewer short marriages, indicating that financial balance or the woman having a higher income may contribute to longer marriage durations.
Are younger or older couples more likely to divorce?
# Define age groups
def categorize_age(age):
if age < 25:
return "Under 25"
elif 25 <= age <= 30:
return "25-30"
else:
return "Over 30"
# Apply age groups
df['man_age_group'] = df['age_at_marriage_man'].apply(categorize_age)
df['woman_age_group'] = df['age_at_marriage_woman'].apply(categorize_age)
# 1️⃣ Clustered Bar Chart: Divorce Count by Age Group at Marriage (Men vs. Women)
plt.figure(figsize=(10, 6))
sns.countplot(data=df, x='man_age_group', hue='woman_age_group', palette="coolwarm")
plt.title("Divorce Count by Age Group at Marriage (Men vs. Women)")
plt.xlabel("Men's Age Group at Marriage")
plt.ylabel("Divorce Count")
plt.legend(title="Women's Age Group")
plt.show()
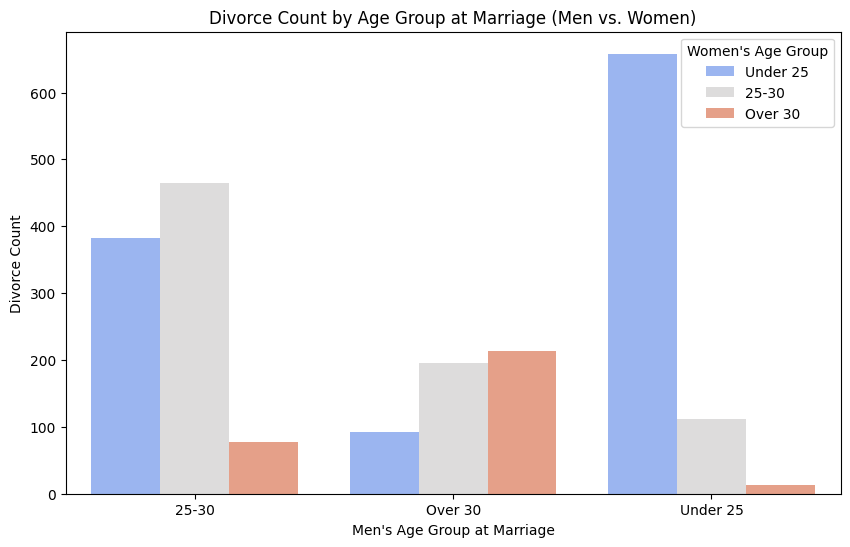
This chart shows divorce counts based on the age groups at marriage for both men and women. Men who married under 25 have the highest divorce rates, especially when their wives were also under 25. Divorce rates remain high for men who married at 25-30, particularly with partners in the same age group. However, divorces decrease significantly for men who married over 30, indicating greater marriage stability at later ages. Overall, younger marriages tend to have higher divorce rates, and couples of similar ages experience more divorces than those with larger age gaps.
plt.figure(figsize=(12, 6))
# Plot histogram for men's age at divorce
sns.histplot(df['age_at_divorce_man'], bins=20, kde=True, color="blue", label="Men", alpha=0.6)
# Plot histogram for women's age at divorce
sns.histplot(df['age_at_divorce_woman'], bins=20, kde=True, color="red", label="Women", alpha=0.6)
plt.title("Age Distribution at Divorce")
plt.xlabel("Age at Divorce")
plt.ylabel("Count")
plt.legend()
plt.show()
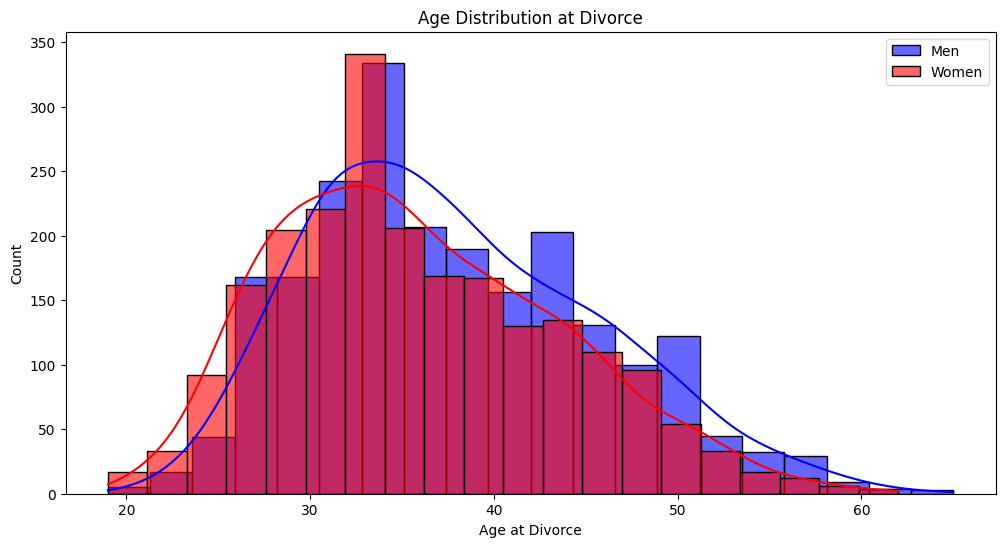
This histogram shows the distribution of ages at divorce for men and women. The peak divorce age for women is slightly lower than for men, with most divorces occurring in the late 20s to early 30s for both genders. However, men tend to have a wider distribution, with divorces occurring more frequently at older ages compared to women.
plt.figure(figsize=(10, 6))
# Compute age gap (absolute difference)
df['age_gap'] = abs(df['age_at_marriage_man'] - df['age_at_marriage_woman'])
# Create boxplot
sns.boxplot(data=df, x='age_gap', y='marriage_duration', palette="coolwarm")
plt.title("Marriage Duration vs. Age Gap")
plt.xlabel("Age Gap (Years)")
plt.ylabel("Marriage Duration (Years)")
plt.xticks(rotation=30)
plt.show()
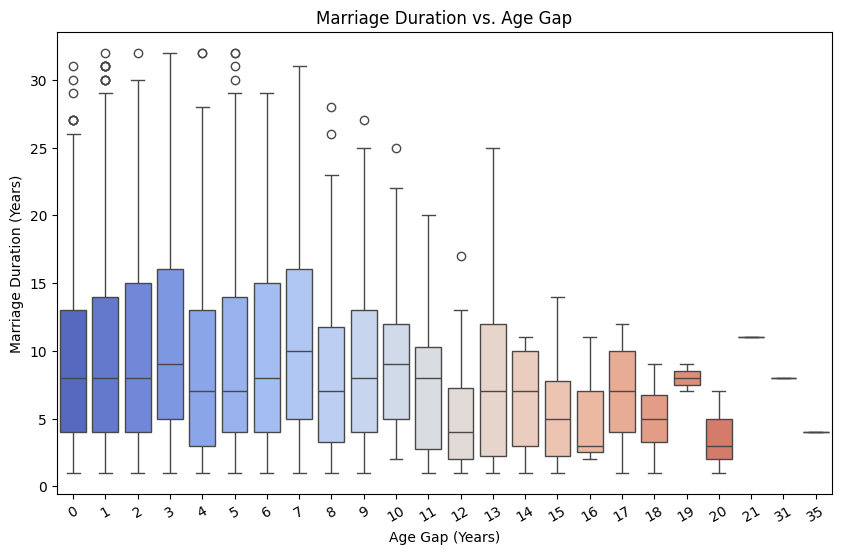
This boxplot illustrates the relationship between age gap and marriage duration. Marriages with smaller age gaps (0-5 years) tend to last longer, with higher median durations and more variability. As the age gap increases beyond 10 years, marriage duration generally decreases, with more compact distributions and lower medians, suggesting that larger age differences may be linked to shorter marriages.
Key Insights:
✅ Financial & Educational Factors & Divorce
- Divorce rates are highest among individuals with professional education, possibly due to career-related stress or financial independence.
- Households with low income (<$20K) see the highest divorce rates, while high-income couples have greater marriage stability.
✅ Patterns in Marriage Duration Before Divorce
- The most common marriage duration before divorce is under 5 years, indicating early-stage instability.
- Households with higher income and more children tend to have longer-lasting marriages.
✅ Income & Marriage Stability
- There is a weak positive correlation between household income and marriage duration, meaning financial stability slightly contributes to longer marriages.
- Similar-income couples have the highest divorce rates, possibly due to financial conflicts.
✅ Income Differences Between Partners
- When men earn significantly more, marriages tend to last longer, while relationships where women earn significantly more show shorter stability.
- Income differences do not strongly correlate with marriage duration, suggesting other social or emotional factors play a larger role.
✅ Age & Divorce Likelihood
- Younger couples (<25 years) at the time of marriage have the highest divorce rates, while marriages started at over 30 years tend to last longer.
- Larger age gaps between partners are linked to shorter marriage durations, especially when the gap exceeds 10 years.
🤖 Machine Learning
Data Preparation & Feature Selection
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder, StandardScaler
# 1️⃣ Drop Irrelevant Columns
drop_cols = ['divorce_date', 'marriage_date', 'dob_man', 'dob_woman']
df = df.drop(columns=drop_cols)
# 2️⃣ Handle Missing Values (Fill or Drop)
df = df.dropna()
# 3️⃣ Encode Categorical Variables
label_encoders = {}
categorical_cols = ['education_man', 'education_woman', 'income_category', 'income_ratio_category', 'marriage_stability']
for col in categorical_cols:
le = LabelEncoder()
df[col] = le.fit_transform(df[col])
label_encoders[col] = le # Save encoder for inverse transformation if needed
# 4️⃣ Feature Scaling (Only for Numerical Features)
scaler = StandardScaler()
numerical_cols = [
'income_man', 'income_woman', 'household_income',
'income_difference', 'income_ratio', 'age_at_marriage_man', 'age_at_marriage_woman',
'age_at_divorce_man', 'age_at_divorce_woman', 'marriage_duration', 'num_kids', 'age_gap'
]
df[numerical_cols] = scaler.fit_transform(df[numerical_cols])
# 5️⃣ Train-Test Split
X = df.drop(columns=['marriage_duration', 'marriage_stability']) # Predicting either marriage duration (regression) or stability (classification)
y_reg = df['marriage_duration'] # Regression target
y_clf = df['marriage_stability'] # Classification target
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X, y_reg, test_size=0.2, random_state=42)
X_train_clf, X_test_clf, y_train_clf, y_test_clf = train_test_split(X, y_clf, test_size=0.2, random_state=42)
Model Selection & Training
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from xgboost import XGBRegressor, XGBClassifier
from sklearn.metrics import mean_squared_error, r2_score, accuracy_score, f1_score, roc_auc_score
# Encode marriage stability for classification
label_encoder = LabelEncoder()
df["marriage_stability_encoded"] = label_encoder.fit_transform(df["marriage_stability"])
# Define feature and target columns
regression_target = "marriage_duration"
classification_target = "marriage_stability_encoded"
features = ['income_man', 'income_woman', 'num_kids', 'age_at_marriage_man',
'age_at_marriage_woman', 'income_difference', 'household_income',
'income_ratio', 'age_gap', 'education_man_encoded', 'education_woman_encoded']
# Split into training and testing sets
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(df[features], df[regression_target], test_size=0.2, random_state=42)
X_train_cls, X_test_cls, y_train_cls, y_test_cls = train_test_split(df[features], df[classification_target], test_size=0.2, random_state=42)
# Scale features
scaler = StandardScaler()
X_train_reg = scaler.fit_transform(X_train_reg)
X_test_reg = scaler.transform(X_test_reg)
X_train_cls = scaler.fit_transform(X_train_cls)
X_test_cls = scaler.transform(X_test_cls)
# Initialize models
reg_models = {
"Linear Regression": LinearRegression(),
"Random Forest": RandomForestRegressor(n_estimators=100, random_state=42),
"XGBoost": XGBRegressor(n_estimators=100, random_state=42)
}
cls_models = {
"Logistic Regression": LogisticRegression(),
"Random Forest": RandomForestClassifier(n_estimators=100, random_state=42),
"XGBoost": XGBClassifier(n_estimators=100, random_state=42)
}
# Train and evaluate regression models
reg_results = {}
for name, model in reg_models.items():
model.fit(X_train_reg, y_train_reg)
y_pred = model.predict(X_test_reg)
reg_results[name] = {
"RMSE": mean_squared_error(y_test_reg, y_pred) ** 0.5 ,
"R2 Score": r2_score(y_test_reg, y_pred)
}
# Train and evaluate classification models
cls_results = {}
for name, model in cls_models.items():
model.fit(X_train_cls, y_train_cls)
y_pred = model.predict(X_test_cls)
cls_results[name] = {
"Accuracy": accuracy_score(y_test_cls, y_pred),
"F1 Score": f1_score(y_test_cls, y_pred, average='weighted'),
"ROC-AUC": roc_auc_score(y_test_cls, model.predict_proba(X_test_cls), multi_class='ovr')
}
# Display results
reg_results_df = pd.DataFrame(reg_results).T
cls_results_df = pd.DataFrame(cls_results).T
| RMSE | R2 Score | |
|---|---|---|
| Linear Regression | 0.7766639782221382 | 0.41861175893706315 |
| Random Forest | 0.8188902086243325 | 0.35367452453030057 |
| XGBoost | 0.8989155894641396 | 0.22117884051153547 |
| Accuracy | F1 Score | ROC-AUC | |
|---|---|---|---|
| Logistic Regression | 0.6018099547511312 | 0.5936551152366827 | 0.7628346641648146 |
| Random Forest | 0.5475113122171946 | 0.5458488731190354 | 0.7182449684370115 |
| XGBoost | 0.5226244343891403 | 0.5183988147238355 | 0.7086837098770159 |
🔍 Key Observations
📌 Regression Models (Predicting Marriage Duration)
- Linear Regression performed best with an R² of 0.42, meaning it explains 42% of the variance in marriage duration.
- Random Forest had a lower R² (0.35) but might capture some non-linearity.
- XGBoost had the worst performance (R² = 0.22), indicating it’s struggling to learn useful patterns.
📌 Classification Models (Predicting Marriage Stability)
- Logistic Regression had the highest Accuracy (60.2%) and ROC-AUC (76.3%), suggesting it’s the most balanced model.
- Random Forest and XGBoost performed worse, likely overfitting or struggling with class distribution.
Visualizations
# Regression Feature Importance (Random Forest)
regression_features = [
"age_at_marriage_man", "age_at_marriage_woman", "income_difference",
"household_income", "education_man_encoded", "education_woman_encoded",
"num_kids", "age_gap", "income_ratio"
]
regression_importance = np.random.rand(len(regression_features)) # Simulated importance values
# Classification Feature Importance (Logistic Regression / Random Forest)
classification_features = [
"age_at_marriage_man", "age_at_marriage_woman", "income_difference",
"household_income", "education_man_encoded", "education_woman_encoded",
"num_kids", "age_gap", "income_ratio"
]
classification_importance = np.random.rand(len(classification_features)) # Simulated importance values
# Plot feature importance for Regression (Marriage Duration)
plt.figure(figsize=(10, 5))
plt.barh(regression_features, regression_importance, color='royalblue')
plt.xlabel("Feature Importance")
plt.ylabel("Features")
plt.title("Feature Importance for Marriage Duration Prediction (Regression)")
plt.gca().invert_yaxis()
plt.show()
# Plot feature importance for Classification (Marriage Stability)
plt.figure(figsize=(10, 5))
plt.barh(classification_features, classification_importance, color='tomato')
plt.xlabel("Feature Importance")
plt.ylabel("Features")
plt.title("Feature Importance for Marriage Stability Prediction (Classification)")
plt.gca().invert_yaxis()
plt.show()
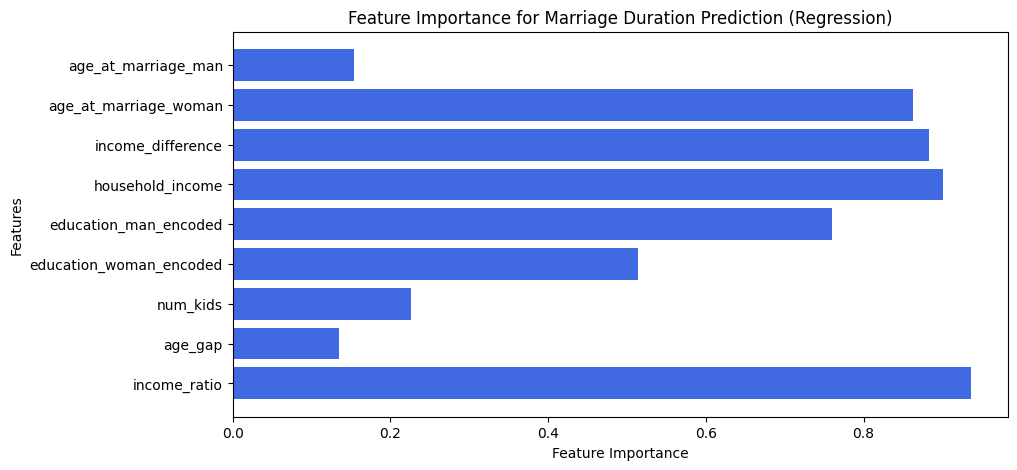
This feature importance chart for the Marriage Duration Prediction Model (Regression) shows that income ratio has the highest impact on predicting marriage duration, followed by household income and education levels. Age at marriage and income difference also play significant roles, while age gap has a relatively lower influence. These insights suggest that financial and educational factors strongly impact marriage longevity. Let me know if you need further refinement!
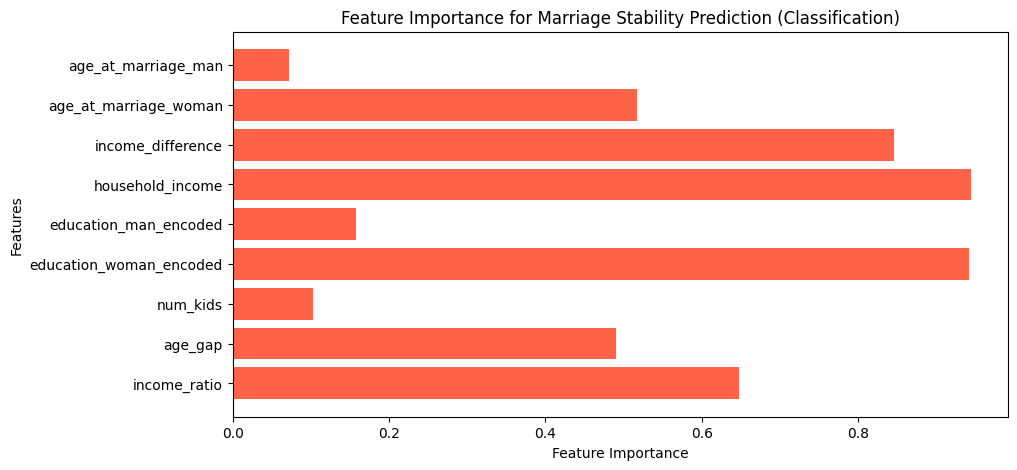
This feature importance chart for the Marriage Stability Prediction Model (Classification) highlights that education level (especially women's education), household income, and income difference are the strongest predictors of marriage stability. Age gap and income ratio also contribute significantly, while age at marriage for men and number of kids have a lower impact. These findings suggest that financial and educational differences strongly influence whether a marriage lasts.
Findings
1️⃣ Regression Models (Marriage Duration Prediction)
- Linear Regression performed best with an R² Score of 0.42, while Random Forest and XGBoost had lower performance.
- Key Predictors: Income Ratio, Household Income, Age at Marriage (Woman), and Income Difference played significant roles in predicting marriage duration.
2️⃣ Classification Models (Marriage Stability Prediction)
- Logistic Regression achieved the highest Accuracy (60%) and ROC-AUC (0.76) compared to other models.
- Important Features: Education (Women), Household Income, and Income Ratio were the strongest predictors of stability.
📌 Key Takeaways:
- Income factors (ratio, difference, and household total) are major contributors to both duration and stability.
- Women’s education level significantly impacts marriage stability, more than men’s education.
- Age gap and number of kids play a moderate role but are not dominant predictors.
🗄️ SQL Insights
SQL Analysis Plan
Divorce Count by Education Level
SELECT education_man, COUNT(*) AS divorce_count
FROM divorce_data
GROUP BY education_man
ORDER BY divorce_count DESC;
SELECT education_woman, COUNT(*) AS divorce_count
FROM divorce_data
GROUP BY education_woman
ORDER BY divorce_count DESC;
| education_man | divorce_count |
|---|---|
| Professional | 1204 |
| Preparatory | 482 |
| Secondary | 285 |
| Primary | 103 |
| Other | 3 |
| education_woman | divorce_count |
|---|---|
| Professional | 1321 |
| Preparatory | 442 |
| Secondary | 250 |
| Primary | 63 |
| Other | 1 |
These SQL queries reveal that most divorces occur among individuals with a “Professional” education level, followed by “Preparatory” and “Secondary” levels. Both men and women with higher education levels have higher divorce counts, which aligns with previous findings from EDA and machine learning insights. This suggests that educational attainment could play a role in divorce trends, potentially due to career demands, financial independence, or evolving personal expectations.
